زاویه

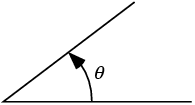
از چرخش نیم خطی حول راسش، ناحیه ای تشکیل می شود که زاویه نامیده می شود. این چرخش را می توانیم ساعتگرد یا پادساعتگرد معرفی کنیم، اما در قضیه مثلثات جهت دوران برای ایجاد یک زاویه پادساعتگرد است و چنین زاویه ای را زاویه مثلثاتی مینامند. اگر نیم خطی را حول راسش به گونه ای بچرخانیم که بازهم به نقطه شروع چرخش برگردد زاویه کامل یا تمام صفحه را تشکیل می دهیم. بنابراین یک دایره به خودی خود، یک زاویه کامل(دوران کامل) می باشد. همینطور، اگر نیم خط را بگونه ای چرخش دهیم که یک نیم رایره به مرکز راسش راطی بنماید، زاویه ای نیم صفحه تشکیل خواهد شد. زاویه را با راس یا نام بردن راس و دو ضلعش می شناسند.

ناگفته نماند، زاویه ها را بکمک وسیله ای بنام نقاله اندازه گیری مینمایند که بر اساس درجه مقیاس بندی شده اند.

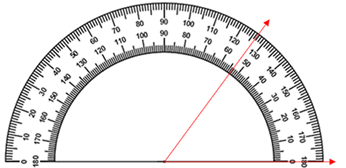
واحد های اندازه گیری زاویه: درجه

واحد های اصلی جهت اندازه گیری زاویه شامل: اول از همه درجه سپس رادیان و در آخر گراد است که در ادامه برای شما توضیح خواهیم داد:

درجه:

اگر ما محیط یک هر دایره ای را به 360  تکه ی همانند قاچ کنیم، هر قاچ را یک درجه نام گذاری میکنند. یعنی یک درجه یک سیصد و شستم محیط یک دایره می باشد.

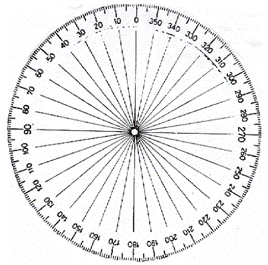
جهت نمایش درجه از نشان ° بهره وری می گردد. برای همین میشود گفت:

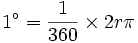
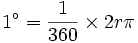
بنابراین در این مقیاس، زاویه که یک صفحه کامل از یک دوران است، برابر 360 درجه و زاویه نیم صفحه هم قاعدتاً برابر 180 درجه می باشد.

بکار گیری واحد درجه(degree) جهت اندازه گیری زاویه، بخاطر بابلی ها بود، که با دستگاه اعداد در مبنای 60 کار می کردند. یعنی هر رقم، تا 60 میرفت و سپس رقم دوم تشکیل میشد.  همچنین 360 درجه شاید از تعداد روزهای یکسال نشات گرفته بود، یعنی آنها در 12 ماه 30 روزه زندگی می کردند.

جزئیات درجه:

همانطور که آگاه هستید، تقریبا همیشه، هر واحدی شامل اجزایی می شود. درجه هم به عنوان یک واحد اندازه گیری شامل اجزایی می شودکه دقیقه و ثانیه می باشند.(این جزء ها، گاهی آرک دقیقه:Arc minute و آرک ثانیه:Arc second هم نامیده می شوند.)

هر دقیقه میشود یک شصتم درجه. 1/60

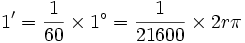
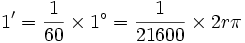
هر ثانیه می شود یک شصتم دقیقه1/60  یا یک سه هزار و شسصدم درجه.  1/3600

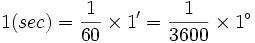
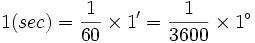
برای نمونه، مثلا اندازه زاویه ای 37 درجه را 30 دقیقه و 15 ثانیه می نویسیم:

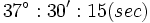
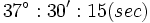
گراد

اگر محیط دایره ای را به 400 قاچ یکسان تقسیم کنیم، هر قاچ را یک گراد می نامند. به زبانی دیگر، یک چهارصدم یک دوران کامل، زاویه ای به اندازه ی یک گراد تشکیل می دهد.گراد را گاهاً گون هم می نامند. برای نمایش گراد از سمبل«gr» بهره وری می شود. برای همین میشود گفت:

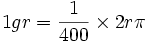
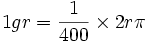
در نتیجه، در این مقیاس اندازه زاویه تمام صفحه یا یک دور کامل 400 گراد و اندازه زاویه نیم صفحه قاعدتاً 200 گراد می شود.

جزئیات  گراد:

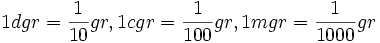
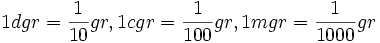
اجزای گراد شامل دسی گراد(dgr) ، سانتی گراد(cgr)، میلی گراد(mgr) که هر یک به ترتیب یک دهم گراد، یک صدم گراد و یک هزارم گراد خواهند بود.

برای نمونه اگر اندازه زاویه ای 37 گراد و 2 دسی گراد و 8 میلی گرا شود،  داریم :

37.208 gr

استفاده از این واحد برای زاویه در ریاضیات خیلی کم است.

رادیان

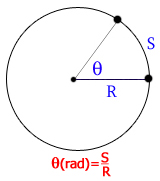
دایره ای به شعاع L را تصور کنید. می دانیم محیط این دایره “دو پی” می باشد. یک رادیان اندازه زاویه مرکزی مقابل به کمانی از دایره می باشد که طول کمان روبرویش به آن برابر شعاع دایره می باشد.

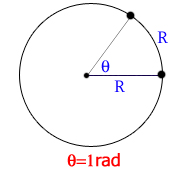
جهت نمایش رادیان از نماد«rad» استفاده خواهیم کرد. در نتیجه  محیط هر دایره برحسب رادیان ” دو π” رادیان می باشد و زاویه نیم صفحه برابر رادیان خواهد بود. پس:

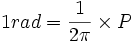
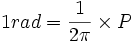
 که در آن P محیط دایره می باشد.

با بهره گیری از تعریف رادیان می شود این نتیجه حاصل شود که اگر طول کمان روبرو به زاویه  برابر s و شعاع دایره r باشد بنابراین اندازه زاویه تتا بر مبنای رادیان را می توان با یک تناسب ساده چنین بدست آورد:

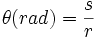
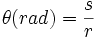
برای نمونه، می خواهیم بدانیم اندازه زاویه مرکزی مقابل به کمانی از دایره که طول آن کمان یک ششم محیط دایره است چند رادیان می باشد؟

روش حل بدون استفاده از فرمول(اساس یافتن فرمول فوق) به این صورت است: r=طول شعاع

برای بهتر شدن ریاضی خود، از مقطع ابتدایی تا مقطع دکترا، با ما تماس بگیرید

اگر طول کمان مساوی 2π باشد پس  اندازه زاویه برابر است با 2π رادیان اما اگر

طول کمان برابر   باشد اندازه زاویه دقیقا چقدر خواهد شد؟

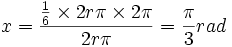
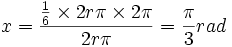
باید گفته شود که که پر کاربرد ترین واحد اندازه گیری زاویه رادیان می باشد که به ویژه در مثلثات، حساب، فیزیک کاربرد فراوان خواهد داشت.

تبدیل واحد های اندازه گیری زاویه به یکدیگر:

دایره ای به شعاع r و زاویه  را در دایره تصور کنید:

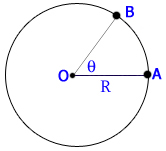
تصور کنید اندازه زاویه  بر اساس درجه D، برحسب گراد G و برحسب رادیان R باشد. با استفاده از تناسب خواهیم داشت:

طول کمان	اندازه زاویه برحسب درجه
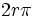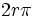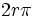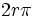	360
	D

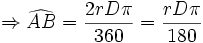
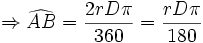
طول کمان	اندازه کمان برحسب گراد
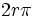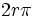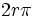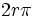	400
	G

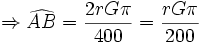
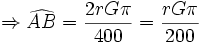
طول کمان	اندازه زاویه برحسب رادیان
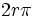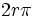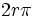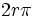	R

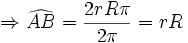
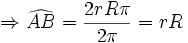
از معادلات بالا این نتیجه را می گیریم

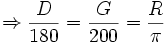
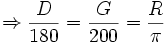
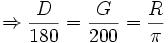
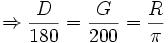
انواع زاویه ها:

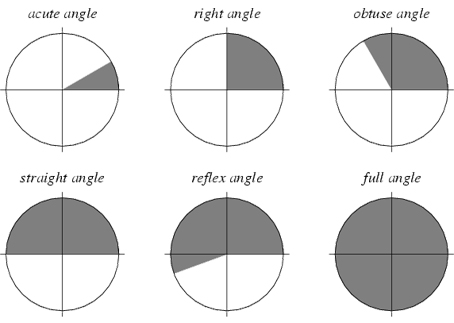
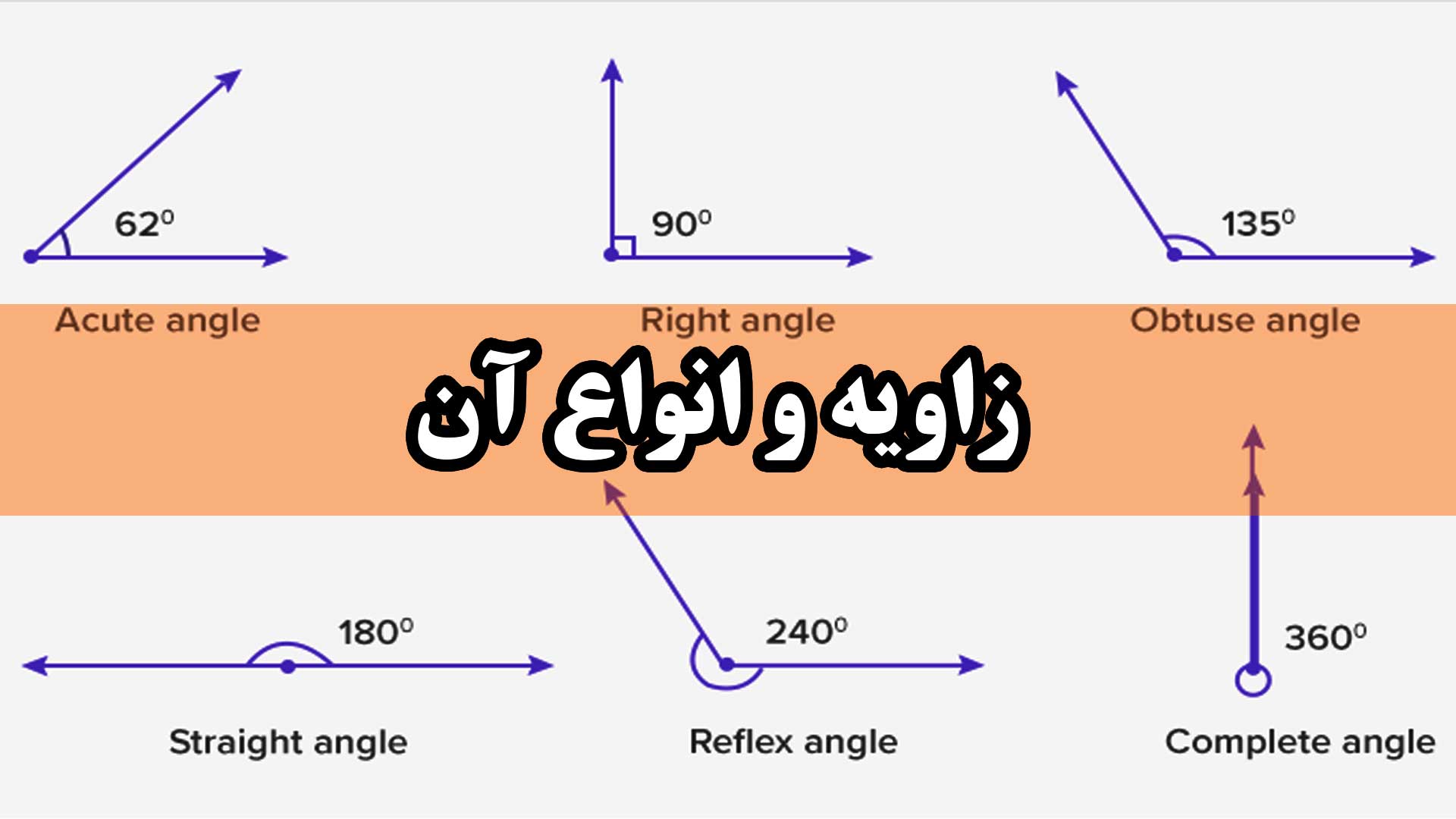
زاویه ها را با توجه به مقدارشان به این صورت طبقه بندی می کنند:

زاویه ها را با توجه به مقدارشان به این صورت طبقه بندی می کنند:

زاویه تند:(acute angle) زاویه θ را تند یا حاده میگوییم هرگاه اندازه اش کمتر از 90 در جه باشد. به
عبارت دیگر:  θ<90

زاویه راست:(right angle) زاویه θ را راست یا قائم میگوییم هرگاه اندازه آن برابر 90 در جه باشد. به
عبارت دیگر: θ= 90 

زاویه باز:(obtuse angle) زاویه θ را باز یا منفرجه می گوییم هرگاه بزرگتر از 90 درجه و کمتر از 180 درجه باشد. به عبارت دیگر:

90<θ<180

زاویه نیم صفحه:(straight angle) زاویه θ را نیم صفحه میگوییم هرگاه برابر 180 درجه باشد. به عبارت دیگر: θ = 180

زاویه بازتاب:(reflex angle) زاویه θ را زاویه بازتاب میگوییم هرگاه بزرگتر از 180 درجه و کمتر از 360 درجه باشد. به عبارت دیگر:

180<θ<360

زاویه کامل:(full angle) زاویه θ را کامل یا تمام صفحه می گوییم هرگاه برابر 360 درجه باشد. به عبارت
دیگر:. Θ = 360