مکان هندسی از مجموعه نقاطی تشکیل شده از صفحه یا فضا می باشد که دارای حداقل یک ویژگی مشترکی باشند. به زبانی دیگر، هر نقطه در این مجموعه دارای این ویژگی خواهد بود و هر نقطه ای که این ویژگی را در خود داشته باشد، عضوی از این مجموعه خواهد بود. پس با این تفسیر، با تعریف این مفهوم قادر خواهیم بود، تعاریف را ساده تر بیان کنیم.
بدست آوردن مکان هندسی
برای نمونه می توان دایره را به شکل زیر تعریف کرد:
مکان هندسی نقطه هایی از صفحه که از یک نقطه ثابت بنام مرکز دایره، به یک اندازه می باشند دایره می نامیم. با این تفاسیر می توانیم بگوییم، هر نقطه شامل این مکان هندسی از یک نقطه ثابت بنام مرکز دایره به یک فاصله مشخصی می باشد. هر نقطه ای که شامل این ویژگی در یک صفحه باشد، شامل این مکان هندسی خواهد بود.
از دیگر ویژگی های این قضیه آن است که با بهره گیری از آنها می توان به سادگی برای اشکال هندسی معادله نوشت.
برای ثبت نام دوره های کنکور، دوره ی دوم و اول با ما تماس بگیرید.
برای نمونه با توجه به تعریف دایره می توان معادله آن را چنین نوشت:
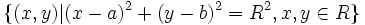
که در آن a طول و b عرض مزکز دایره و R شعاع دایره می باشد.
برای مشخص کردن این مکان می شود به این صورت عمل نمود:
1- به اندازه کافی نقطه هایی را که در خصوصیت داده شده مشترک هستند، پیدا کنیم.
2- نقاط پیدا شده را به همدیگر وصل می کنیم، تا تصویری شهودی که دنبال آن بودیم، پیدا کنیم.
3- مکان هندسی را تعریف خواهیم کرد. بعد آن، چک کنیم، که آیا هر نقطه در کل نقاطی که پیدا کردیم، در خصوصیت ذکر شده، صدق می کنید یا خیر، برعکس، آیا هر نقطه که در این خصوصیت صدق می کند در مجموعه ای که پیدا کردید، وجود دارد یا خیر؟
هیچ دیدگاهی نوشته نشده است.